Stern-Gerlach Devices in Series
The Abstract Vector Space of Quantum States
Spin is an orientation inherent to individual particles, and is typically observed as the direction of their magnetic dipole moments. The Stern-Gerlach device is a machine used to split a beam of silver atoms depending upon their spin. The input is always a single beam of silver atoms. The output is always one or two beams of silver atoms, each with a definite spin. Because the magnitude of a silver atom's spin is $h/4\pi$, the only observable values in any given direction are:
$$\frac{h}{4\pi}\quad \mathrm{or}\quad -\frac{h}{4\pi}.$$
The Stern-Gerlach device splits the beams using a sharply pointed magnetic field that has a distinguished orientation. The output beams of silver atoms are always aligned with or against this orientation. If it aligned with the magnet, we call them spin up, and represent such atoms by the quantum state vector $|\uparrow\;\rangle$. If it is aligned against the magnet, we call them spin down, and represent such atoms by the quantum state vector $|\downarrow\;\rangle$.
While the three-dimensional spin vectors of these two beams are linearly dependent in the sense that
$$\overrightarrow{S}_{\uparrow} = - \overrightarrow{S}_{\downarrow},$$
the quantum state vectors are linearly independent. That is,
$$|\uparrow \;\rangle \neq \lambda |\downarrow\;\rangle,$$
for any constant $\lambda$. These quantum state vectors are not vectors in three-dimensional space. They are vectors in a two-dimensional, abstract space of quantum states. Although they are related.
The three-dimensional vectors $\overrightarrow{S}$ define a specific direction in our three-dimensional world. Whereas $|\uparrow\;\rangle$ and $|\downarrow\;\rangle$ can be thought of as representing the two-dimensional spherical shell that corresponds to the direction of spin relative to the Stern-Gerlach magnet. In this sense, the most general state of the individual, input silver atoms is
$$|\, \mathrm{Ag}\,\rangle = \alpha\, |\uparrow\;\rangle + \beta\, |\downarrow\;\rangle,$$
where $\alpha$ and $\beta$ are constants. Last time we explored how $\alpha$ and $\beta$ determine the relative intensities of the spin up and spin down output beams.
For the mathematically inclined reader, $\alpha$ and $\beta$ are complex numbers$^{1}$, each with real and imaginary parts. They are subject to the constraint that
$$|\alpha|^{2} + |\beta|^{2} = 1,$$
which is equivalent to
$$(\mathrm{Re}\,\alpha)^{2} + (\mathrm{Im}\,\alpha)^{2} + (\mathrm{Re}\,\beta)^{2} + (\mathrm{Im}\,\beta)^{2} = 1.$$
This gives one constraint amongst four real variables, yielding a three-dimensional space that can be related to the three-dimensional vector $\overrightarrow{S}$. The relation is not trivial, but hopefully this serves as a motivating visualization.
If you are not yet familiar with complex numbers, don't worry. We will introduce them to you in a future episode, but know that they are central to the study of Quantum Mechanics.
Two Stern-Gerlach Devices
Today we'll consider a variation of the Stern-Gerlach experiment that includes multiple devices connected in series. Thought of as a circuit, they can clarify the main ideas of quantum theory. As a bonus, it serves as a first, simple example of a quantum circuit.
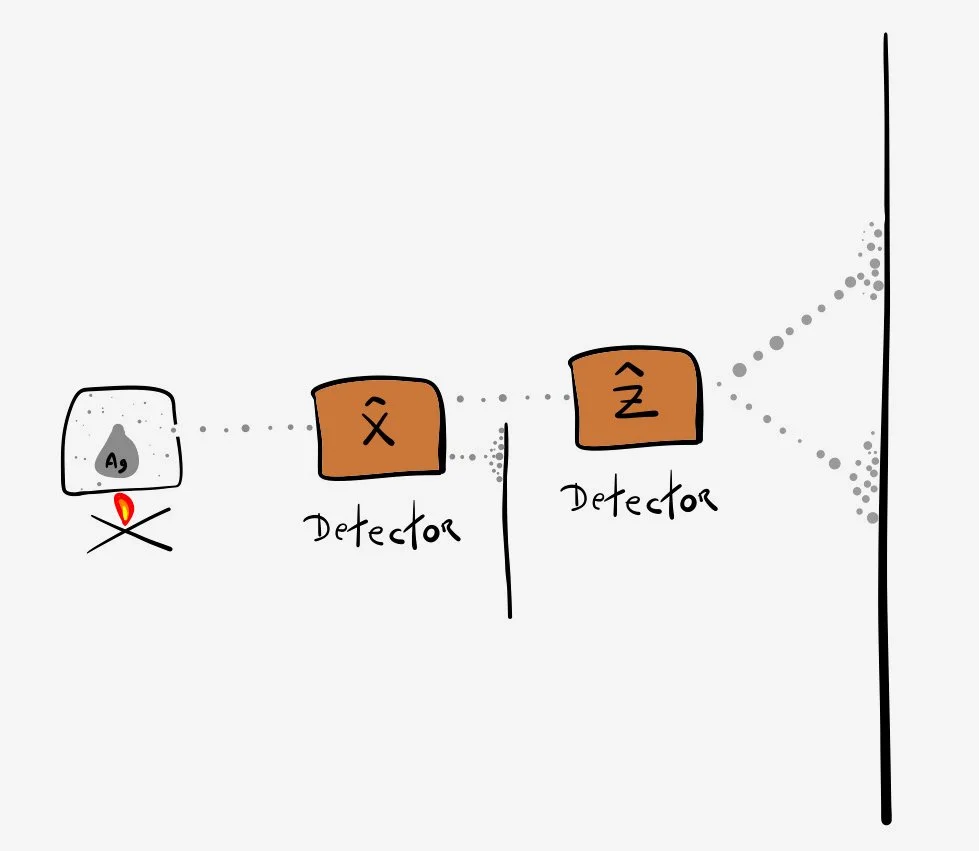
Typically, when considering a circuit of Stern-Gerlach devices, we connect one of the two outputs of a device to the input of the next device. For concreteness, let's consider two Stern-Gerlach devices where the spin up output of the first device serves as the input to the second device. We can do this by putting a screen in front of the spin down output. We will also assume thermal initial conditions for the original input beam. That is, we assume that the spins of the first input beam will be randomly distributed.
In the two-device setup, we have the freedom to choose the direction of both Stern-Gerlach magnets. Let's explore four relevant scenarios.
Two Aligned Devices
For concreteness, let us assume that both devices are aligned in the $\widehat{x}$ direction. In this case, the final output is a single beam pointed in the $\widehat{x}$-direction. That is, the final beam is composed of silver atoms in the $|\uparrow\;\rangle$ configuration. This is not surprising, given that the input to the second device was a beam of pure spin up states.
Two Antialigned Devices
For concreteness, let us assume that the first device is aligned in the $\widehat{x}$-direction. For the second device to be antialigned, it must point in the $-\widehat{x}$-direction. In this case, the final output is a single beam pointed in the $-\widehat{x}$-direction. That is, the final beam is composed of silver atoms in the $|\downarrow\;\rangle$ configuration. This is not surprising, given that the input to the second device was a beam of pure spin up states, and the observing magnet was reversed.
Two Orthogonal Devices
For concreteness, let us assume that the first device is aligned in the $\widehat{x}$-direction, and the second device is aligned in the $\widehat{y}$-direction. In this case, the final output is a pair of beams of equal intensity, both $|\uparrow\;\rangle$ and $| \downarrow \;\rangle$. This is not unlike the initial conditions considered last time with $\varphi = 90^{\circ}$.
Two Unaligned Devices
For concreteness, let us assume that the first device is aligned in the $\widehat{x}$ direction, and the second device is aligned to with a unit vector $\overrightarrow{v}$ at an angle $\varphi$ with respect to $\widehat{x}$. That is,
$$\overrightarrow{v}\cdot \widehat{x} = \cos\varphi.$$
Per our discussion last time, the device will split into two beams with intensities dependent upon $\theta$.
$$|\mathrm{Ag}_{2}\,\rangle = \cos\frac{\varphi}{2} |\uparrow\;\rangle + \sin\frac{\varphi}{2}|\downarrow\;\rangle.$$
Three Devices
We now extend the discussion to consider three Stern-Gerlach devices. The precise details are starting to get complicated, so it might be worth reading over these results multiple times to make sure you understand them. In all cases remember that $|\uparrow\;\rangle$ and $|\downarrow\;\rangle$ are defined with respect to the Stern-Gerlach magnet's direction.
zzz
The case where all three devices are precisely align probably comes as no surprise. Since the output of the second device is purely spin up, the output of the final device is also purely spin up, with respect to $\widehat{z}$, of course.
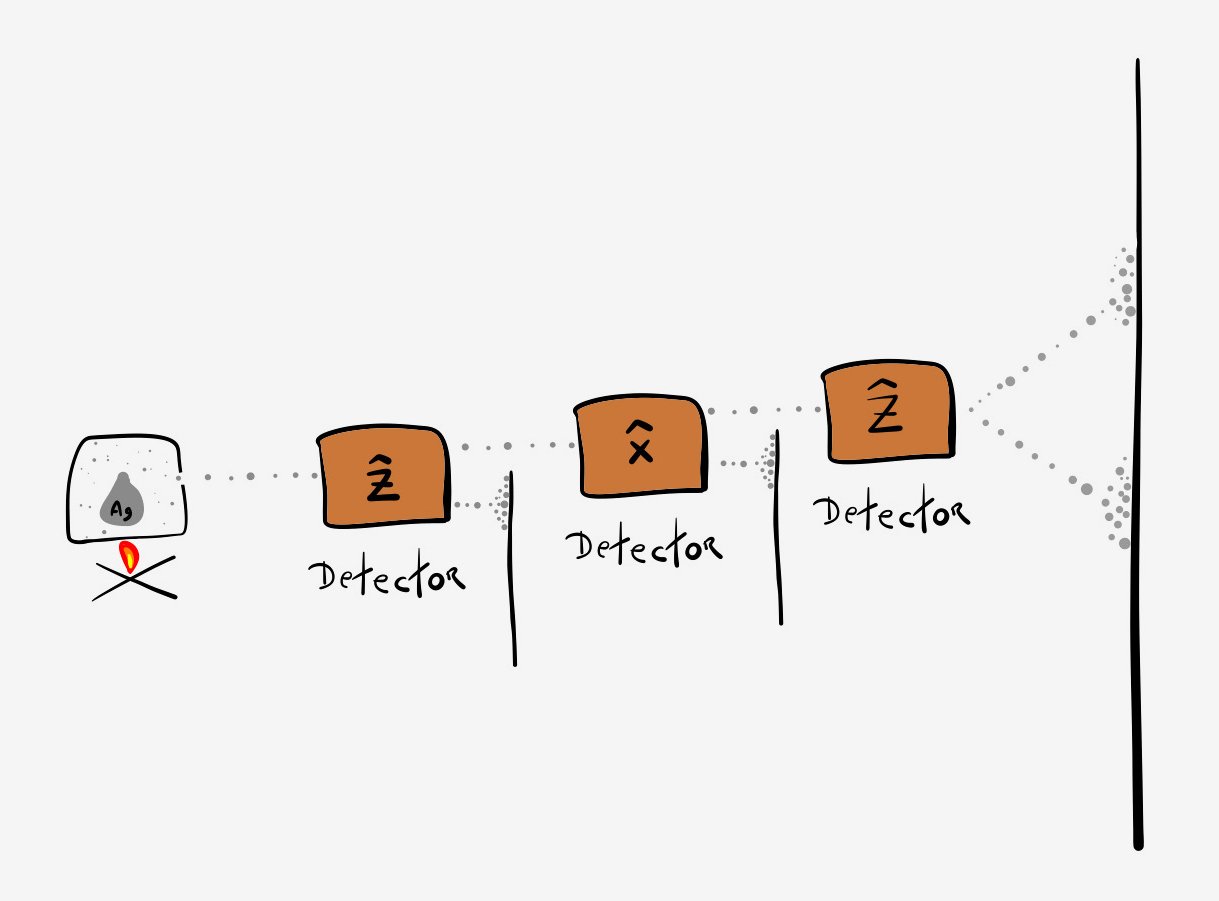
zxz
Given that the second device is orthogonal to the first, the second output splits. Sending only the $|\uparrow\;\rangle$ output - which is up with respect to the $\widehat{x}$-direction, into the final device, which is orthogonal to $\widehat{x}$, we find the final output to be an evenly split beam.
zxx
Given that the second device is orthogonal to the first, the second output again splits. Sending only the $|\uparrow\;\rangle$ output - which is up with respect to the $\widehat{x}$-direction, into the final device, which is aligned with the second, we find the final output to be a single beam, purely in the $|\uparrow\;\rangle$ state, with respect to the $\widehat{x}$-direction.
zzx
Given that the second device is aligned with the first device, the input into the third device is purely $|\uparrow\;\rangle$ with respect to the $\widehat{z}$-direction. Because the third device is orthogonal to the second, the final output will be an evenly split beam.
xyz
All devices are orthogonal. Hence the output of the second device will be evenly split. Since we only send the spin up component of this output into the final device, and the final device is also orthogonal, the final result will be an evenly split beam.
Exercises
Exercise 1 : Compare the two device setup results to those with a single device whose input beam is exposed to a external magnetic field studied last time.
Exercise 2 : Set up a three-device configuration as $z-\theta-z$, where $\theta$ is an arbitrary angle. Vary $\theta$ and describe mathematically how the relative intensities of the final output beams change. You may wish to refer to the last lecture for details.
Exercise 3 : Sometimes it is helpful to be explicit about the how $|\uparrow\;\rangle$ and $|\downarrow\;\rangle$ are aligned in three-dimensional space. Let $|\uparrow_{x}\;\rangle$ be the spin up output of a Stern-Gerlach device aligned in the $\widehat{x}$ direction. Similarly, $|\downarrow_{z}\;\rangle$ is the spin down output of a Stern-Gerlach device orientated in the $\widehat{z}$-direction. Write $|\uparrow_{z}\;\rangle$ explicitly in terms of $|\uparrow_{x}\;\rangle$ and $|\downarrow_{x}\;\rangle$. That is, find the constants $\alpha$ and $\beta$ with respect to the $\widehat{x}$-direction. Do this also for $|\uparrow_{y}\;\rangle$.
Exercise 4 : Compare Stern-Gerlach devices chained in series and polarization filters also chained in series.
Exercise 5 : Consider a three-device setup where we refocus the split beam output of the second device into a single beam that inputs into the third device. Let the first and third device point in the $\hat{z}$-direction. Explain if and how the orientation of the magnet of the second device changes the final outcome.
Notes
$^{1}$ : A complex number involves a pair of real numbers $a$ and $b$ that can be written as
$$a+ib,$$
where the unit imaginary number $i = \sqrt{-1}$.