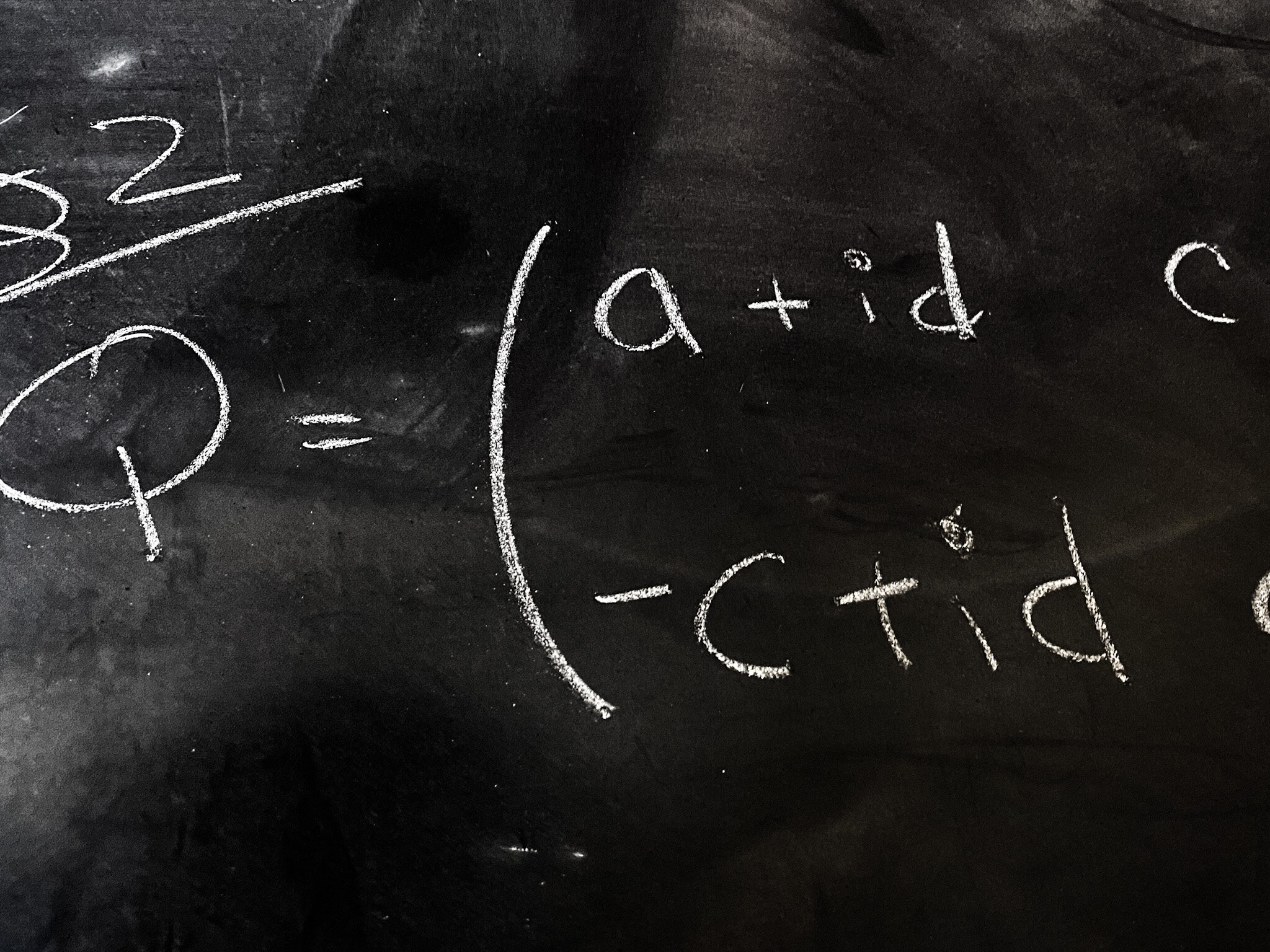
Ahoy! This page uses MathJax to typeset math symbols. If you’re seeing code rather than nice, typeset symbols, you may need to hit “refresh” to render things cleanly.
Applied Representation Theory : 002
Matrix Constructions
We construct each of the normed division algebras A using matrices. We also review some basic properties of matrices, and discuss a few important collections of them.
Matrices
A map between vector spaces is called linear if it preserves vector addition and scalar multiplication. Essentially, a linear map f behaves as
f(a⋅(v+w))=af(v)+af(w),
for a in A.
In the first set of exercises, we considered the space of linear maps from Cn to itself, Homn,nC. These turned out to be the n××n-matrices with complex components. You proved that Homn,nC is a vector space, whose C-dimension is n2.
The subset of invertible n×n-matrices has one restriction, namely:
detM≠0.
This subset is useful and as such has its own name1,
GLnC={M∈Homn,nC|detM≠0}.
From linear algebra, you might recall that the determinant of a matrix is an alternating multilinear function of its columns. For a 2×2 matrix,
M=(abcd)⇒detM=ad−bc.
Similarly, for a 3×3 matrix,
M=(abcdefghj)⇒detM=a(ej−hf)−b(dj−gf)+c(dh−eg),
and so on.
You might also recall that the determinant of a product of matrices is the product of determinants:
det(MNP)=detMdetNdetP.
From this we can immediately see that the subset of invertible matrices is closed under matrix multiplication. Because matrix multiplication itself is an associative operation:
MNP=(MN)P=M(NP),
and the identity matrix 1 is trivially invertible, we have an important result (that you will prove in the exercises):
GLnC with matrix multiplication forms a group.
The general linear group, GLnC, being a subset of Homn,nC is not a vector space2, but is intimately related to Homn,nC. It also has a number of notable subgroups - that is, subsets that are groups under the same multiplication operation. In particular, the special linear group is defined to be the subset of invertible matrices with unit determinant:
SLnC={M∈GLnC|detM=1},
SLnC will feature prominently in future discussions.
Matrix Facts
A few technical reminders about matrices are in order. First, the trace of a matrix is the sum of its diagonal components. Additionally there is the cyclic property of the trace:
Tr(MNP)=Tr(PMN)=Tr(NPM).
Thus if a matrix M is diagonalizable by a similarity transformation S,
M=SΛS−1,
the trace always amounts to the sum of the eigenvalues:
TrM=Tr(SΛS−1)=TrΛ=∑iΛii=∑iλI,
where components of Λij are simply λiδij.
Functions of matrices are defined in terms of their Taylor series. Notably,
eM=∞∑n=01n!Mn.
Amusingly,
deteM=eTrM,
which you can verify as an exercise in matrix algebra.
The Physicists’ σ matrices
The physicists' σ matrices are given by
σ1=(0110),σ2=(0−ii0),σ3=(100−1).
Each of these are traceless and satisfy:
σ†i=σi.
They show up in all sorts of applications.
Let I be the identity matrix and define the matrices
I=iσ1,J=iσ2,K=iσ3.
While trivial, it's hopefully clear that
R≅{c|c∈R}.
Some what less trivially, you can show that
C≅{aI+bJ|a,b∈R}.
Similarly, you can show
H≅{aI+bI+cJ+dK|a,b,c,d∈R}.
Complex and quaternionic conjugation require an operation such that will take
I→−I,J→−J,K→−K.
An operation consistent with all three σ matrices is a transpose together with component-wise complex conjugation:
I→¯IT=−I,J→¯JT=−J,K→¯KT=−K.
This is precisely the same operation that mapped Homn,1A to Hom1,nA
Thus for the involution in C we may write:
¯z→Z†=¯ZT,
in terms of matrices. Here Z is in the real span^{3} of the two matrices 1 and J.
Z∈spanR{1,J}≅C.
Therefore if Z=a1+bJ, we have
Z†Z=(a2+b2)1.
As for the involution in H we have:
¯q→Q†=¯QT.
Where Q is in the real span of the four matrices 1,I,J and K:
Q∈spanR{1,I,J,K},
Thus, for Q=a1+bI+cJ+dK, we have
Q†Q=(a2+b2+c2+d2)1.
These agrees well with the explicit computations:
detZ=det(ab−ba)=a2+b2
detQ=det(a+dc+ib−c+iba−d)=a2+b2+c2+d2.
Exercises
2.1 : Dimensionality
Argue that the nonzero subset of Rn:
Rn×={x∈Rn|x≠0},
is not a vector space. In what sense does Rn have dimension n? How is this space related to GLnC? (Hint: think local vs global.)
2.2 : Matrices of Quaternions
Because the components do not commute, the determinant of a matrix in Homn,nH is tricky to define. For an arbitrary matrix q∈Homn,nH, represent q as a member of Hom2n2,nC. Then take a determinant. Use that definition to verify that q is invertible if and only if detq≠0.
2.3 : Verifying Group Axioms
Look up the axioms for a group and verify explicitly that GLnC is a group. Hence verify that SLnC is a subgroup of GLnC.
2.4 : Vector Spaces vs Groups
Demonstrate that sl2=spanC{σ1,σ2,σ3} is a complex vector space. Why is sl2 a vector space but not SL2C?
2.5 : Matrix Isomorophisms
Prove the vector space isomorphisms (2) and (3) extend to the full algebra structure by identifying algebra multiplication with matrix multiplication.
2.6 : Magnitudes
Verify (5) by explicit computation, and verify that
detQ†Q=(detQ)2=|Q|2.
Hence argue the same for (4). What choice in our definitions forced detQ to be a positive, real number? What happens when we relax that choice? (Hint: See Exercise 2.4.)
1 The GL here standards for “general” and “linear”. The “n” gives the rank of the matrix, alternatively the dimension of the vector space upon which it acts. The word general implicitly points to a specialized linear subset, which we shall visit with soon enough.
2 You might read that GLnC has dimension n2. This is meant as its (topological) dimension as a smooth manifold, i.e. the number of complex parameters that can be used to characterize the space.
3 The span of two vectors is the set of all linear combinations of those two vectors. The same language applies for n vectors. The span of m linearly independent vectors is an m-dimensional vector space. We can explicitly distinguish between R and C spans where appropriate.
©2021 The Pasayten Institute cc by-sa-4.0
