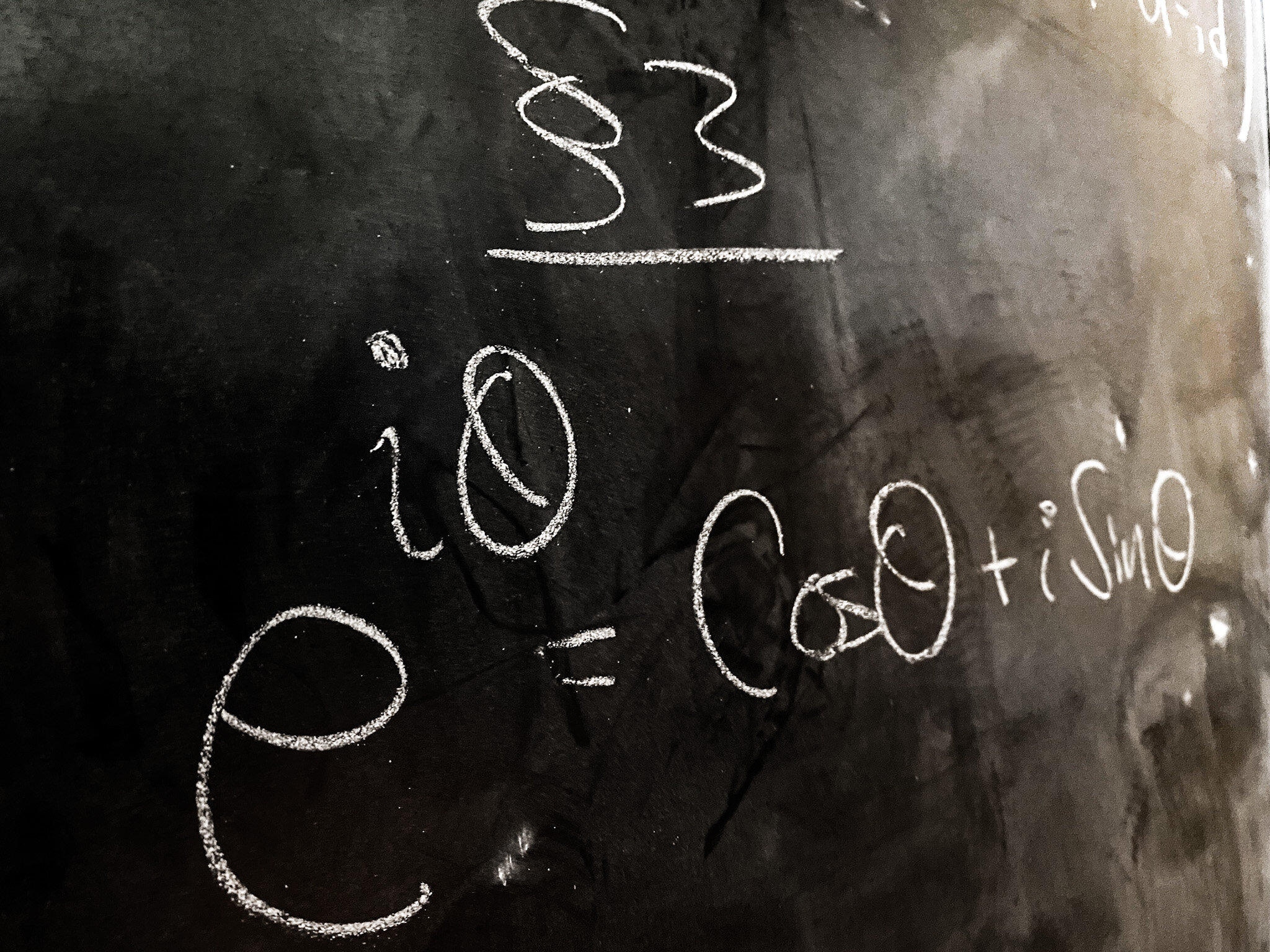
Ahoy! This page uses MathJax to typeset math symbols. If you’re seeing code rather than nice, typeset symbols, you may need to hit “refresh” to render things cleanly.
Applied Representation Theory : 003
The Euler Relation
The complex numbers enjoy a polar representation that gives rise to the famous Euler relation. The angular component is parametrized by the unit circle in C. The quaternions - being a normed vector space - also enjoy a similar representation, although angular component is now parametrized by the three-sphere.
The Commutator
The quaternions are a vector space equipped with a multiplication operation on vectors. Such a space is called an algebra. The multiplication of quaternions does not commute. Instead, basis elements i, j and k, satisfy:
ij−ji=2k,jk−kj=2i,ki−ik=2j.
The lack of commutation is formally captured by the commutator, which for two objects A and B is written
[A,B]=AB−BA.
The idea is that if [A,B]=0, A and B commute. The commutator of i and j is
[i,j]=2k.
Last time we saw how the quaternions could be modeled by traceless, 2×2 complex matrices, the σ matrices:
I=iσ1,J=iσ2,K=iσ3.
This construction of H also satisfies the commutation relations (1):
[I,J]=2K,[J,K]=2I,[K,I]=2J.
Because the abstract basis of quaternions: i,j,k satisfy the same commutation relations as the concrete, matrix basis: I,J,K
we say that the two formulations are algebraically isomorphic. That is to say, they are essentially equivalent constructions. By contrast, R4 and H are isomorphic as vector spaces, but not as algebras1.
The commutation relations that define the matrix representation of H can be expressed compactly in terms of the σ matrices:
[σm,σn]=2iϵmnℓσℓ.
Here m,n,ℓ runs through 1,2,3 and the ϵ symbol is the totally antisymmetric, three index object where
ϵ123=ϵ231=ϵ312=1,ϵ132=ϵ321=ϵ213=−1.
While intricate, this notation is compact and extremely common.
The σ matrices also satisfy set of relations, the so-called anticommutation relations:
{σm,σn}=σmσn+σnσm=2δmn1,
where δmn is the symmetric object where δmn is 1 if m=n and 0 otherwise. It immediately follows that the unit imaginary quaternions satisfy
{i,j}=0,{j,k}=0,{k,i}=0,
which is to say, they anticommute.
This fact proves useful in evaluating products:
(bi+cj+dk)2=−(b2+c2+d2)+bc(ij+ji)+bd(ik+ki)+cd(jk+kj),
so that (4) implies the cross terms vanish
(bi+cj+dk)2=−(b2+c2+d2).
The Euler Relation
Let U1 be the set of complex numbers of unit magnitude:
U1={z∈C||z|=1}.
Complex numbers have a polar decomposition:
z=Reiφ,R=|R|,φ∈[0,2π).
Evidently |z|=|R|, so that the unit complex numbers can alternatively be parametrized by an angle θ.
U1={eiθ∈C|θ∈[0,2π)},
which is equivalent as a set to the unit circle, S1.
The unit complex numbers satisfy the Euler relation:
eiθ=cosθ+isinθ,
which you can readily verify by explicitly expanding the exponential as a series. Recall from our previous discussions that we can represent a complex numbers with 2×2 matrices,
Z=a1+bJ,
where J=iσ2. Specified as a matrix, Z is
Z=(ab−ba),
so that (5) becomes
eiθ=(cosθsinθ−sinθcosθ),
which is precisely the matrix of rotations in the plane. Notice that
detZ=a2+b2=|Z|2,
so that
deteiθ=cos2θ+sin2θ=1.
The Unit Quaternions
Just as the unit complex numbers sweep out a circle in the plane, the unit quaternions sweep out a 3-sphere in R4. Let us see how that might be. For a given quaternion q
q=a+bi+cj+dk.
The unit quaternions are those that satisfy |q|=1. Let us denote the set of these unit quaternions by H1. So,
H1={q∈H||q|=1}
This condition corresponds to the hypersurface in R4 defined by the equation
a2+b2+c2+d2=1.
Let us split q into real and imaginary parts:
q=a+Θ,
where Θ=bi+cj+dk. In the exercises you are asked to verify the Euler relation for imaginary quaternions:
eΘ=cos|Θ|+Θ|Θ|sin|Θ|,
using the commutators of abstract basis elements i,j and k given by (1).
There is another way to motivate the Euler relation (8), using the matrix representation of H.
In the 19th century Jacobi proved that for a complex, square matrix M:
deteM=eTrM.
Since Θ is purely imaginary,
Θ=bI+cJ+dK.
Notice that the σ matrices all have vanishing trace. Therefore the matrices I,J and K are also traceless, so that (9) gives us:
deteΘ=|eΘ|=1.
Therefore, any imaginary quaternion matrix Θ can be exponentiated to give a member of H1.
Exercises
3.1 : Algebras over R4
An algebra is a vector space with a notion of vector multiplication. H is an algebra based on R4, where a generic vector v in R4:
v=aˆe1+bˆe2+cˆe2+dˆe4,
can be multiplied by other vectors following the identifications
ˆe1=1,ˆe2=i,ˆe3=j,ˆe4=k.
i,j and k of course satisfy the commutation relations (1).
There are many possible algebras that can be built from R4. The alternating algebra in four-dimensions demands
ˆeiˆej=−ˆejˆei,
while the symmetric algebra requires
ˆeiˆej=ˆejˆei.
The clifford algebra modifies the alternating algebra somewhat:
ˆeiˆej+ˆejˆei=2δij,
where δij=1 if I=j, and vanishes otherwise. We can even augment the clifford algebra to service four-dimensional Minkowski space:
ˆeμˆeν+ˆeνˆeμ=2ημν,
where off-diagonal terms vanish and ηtt=1 and ηxx=ηyy=ηzz=−1.
Prove that each of these algebras are different - that is, they are not isomorphic - by considering the space of all linearly independent products of basis vectors for each case.
3.2 : Prove the Euler Relation
For a purely imaginary quaternion:
Θ=ib+jc+kd,
verify the Euler relation for quaternions
eΘ=cos|Θ|+Θ|Θ|sin|Θ|.
3.3 : Eigenvalues of I,J,K
Show that the eigenvalues of I,J and K are all ±i. Hence show that the eigenvalues of
Θ=ib+jc+kd,
are ±i|Θ|.
3.4 : Polar Decomposition for H
For a given quaternion q:
q=a+ib+jc+dk,
construct the polar decomposition of q. That is, for any q, find a real number q0 and a totally imaginary quaternion Φ such that
q=q0eΦ.
3.5 : The Exponential Map as a homomorphism
A homomorphism ( say, f) is a map between two groups (say G and H) that preserves the structure of group multiplication:
f:G→H,
where
f(a⋅b)=f(a)⋅f(b).
Argue that U1 is a group under multiplication. Show that it is homomorphic to the additive group of the reals (R,+). Show explicitly that the exponential map is a homomorphism that takes this additive group (R,+)to the multiplicative group (C,×).
3.6 : Quaternions don’t commute
Argue that ImH is a vector subspace of H, and is therefore an additive group under vector addition. We have already seen that the exponential maps ImH to H1. Why does the exponential map fail to to be a homomorphism of groups in this case? For Θ and Φ in ImH, explicitly evaluate both
eΘeΦ,andeΘ+Φ.
Use the Euler relation to compare them explicitly and remark on their difference.
1 Why? Because R4 has no inherent concept of vector multiplication. It is a technical point, to be sure, but one that we need to use often in other contexts.
©2021 The Pasayten Institute cc by-sa-4.0
