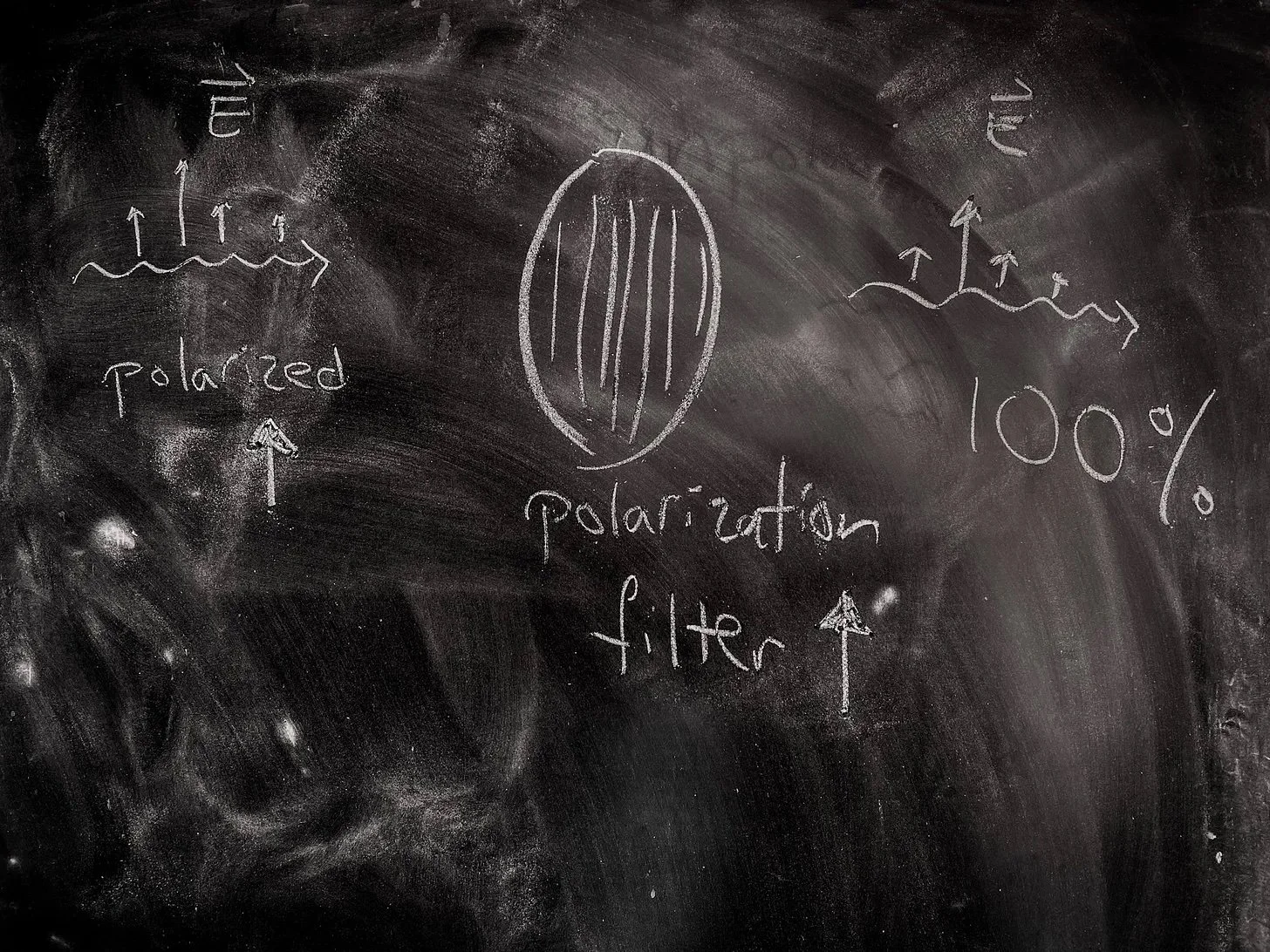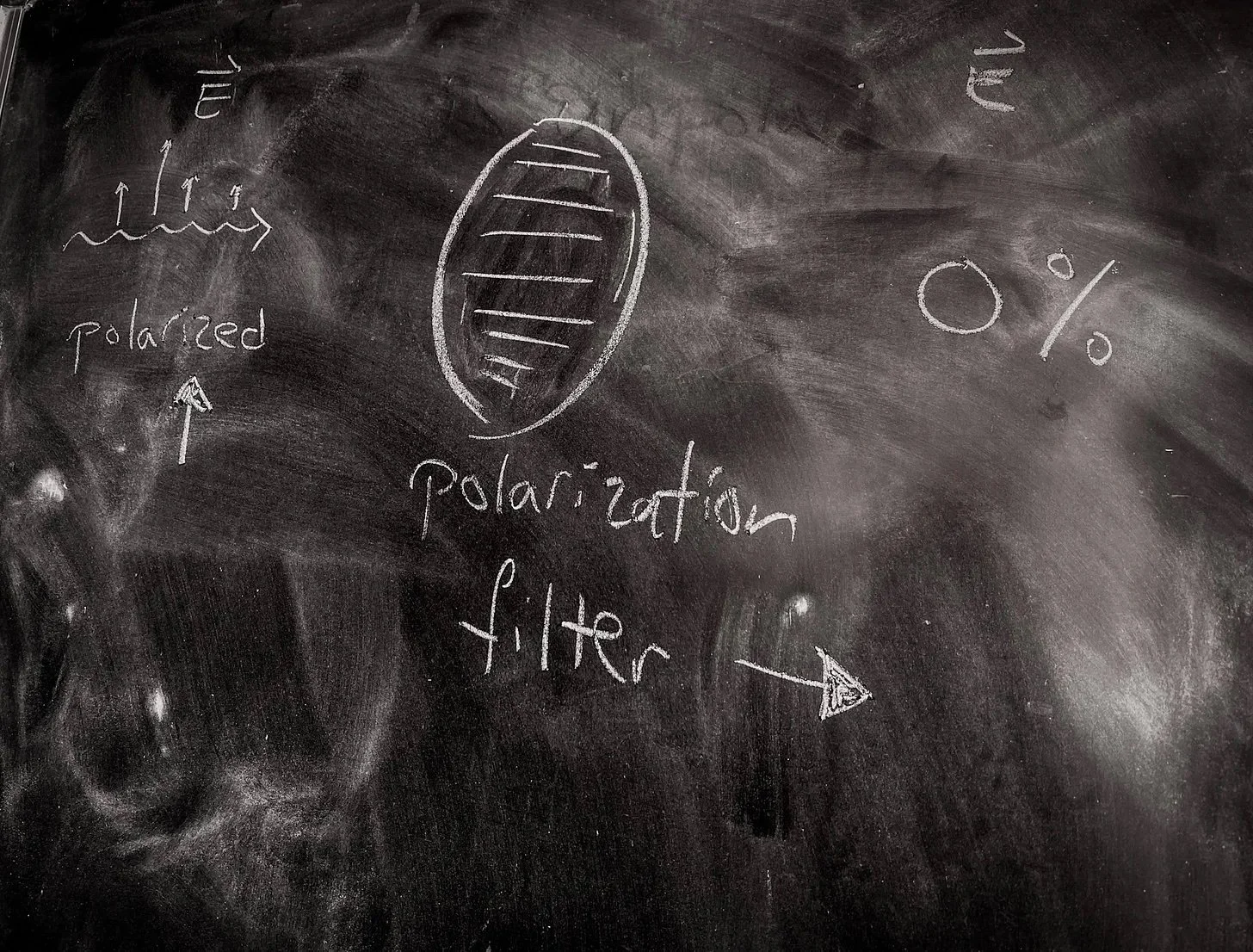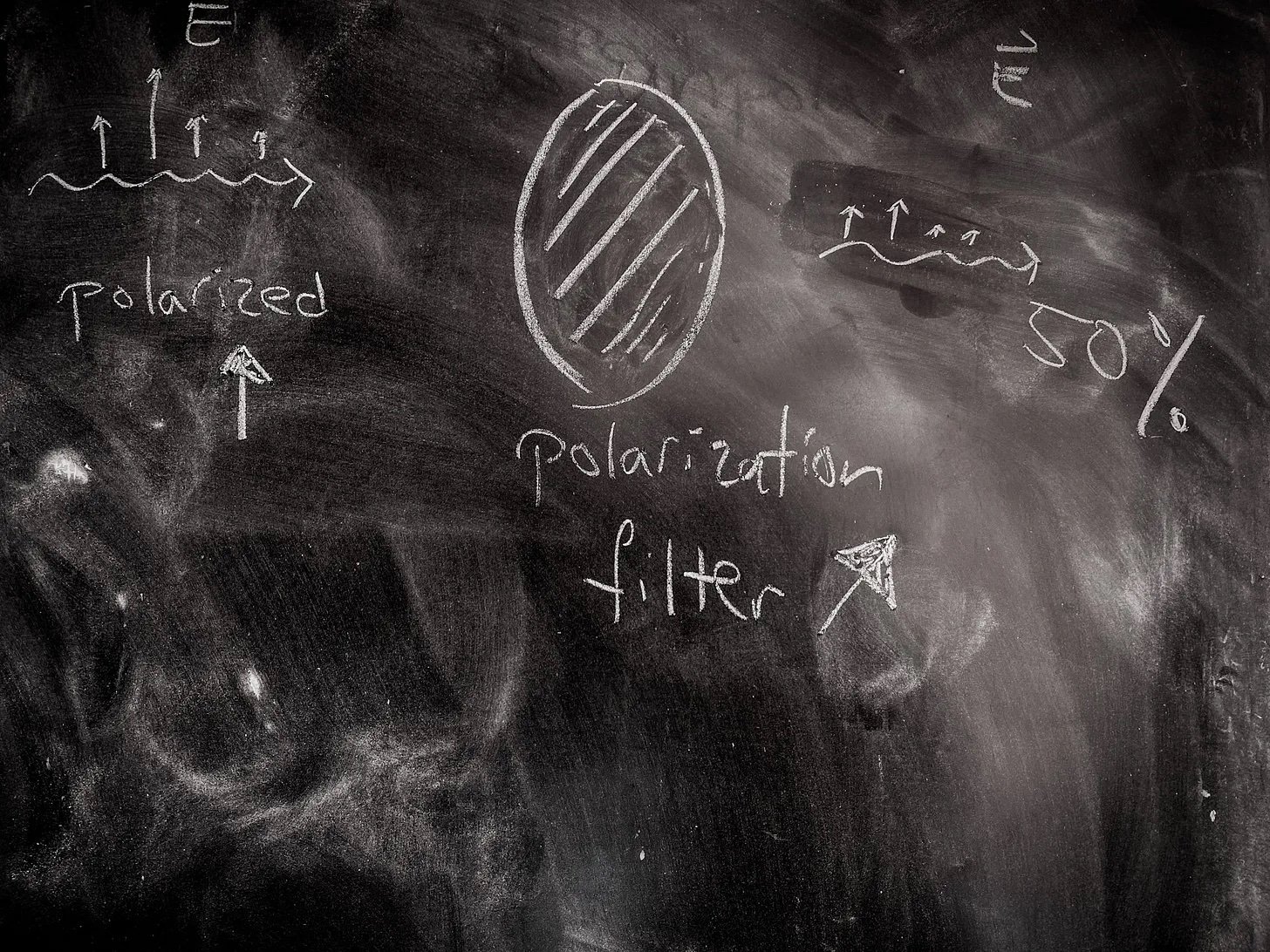Polarization of Photons

We study the polarization of light waves and apply those lessons to the idea of photons. We then see directly how Quantum Mechanics influences our observed reality.

Have you ever tried out a pair polarized sunglasses?

The idea behind a polarization filter is that it reduces the amount of light coming through, typically by half.

Light - you know, electromagnetic waves - can have two polarization modes, both of which are orthogonal to its direction of motion. One way to think about it is asking: which direction does the electric field point?

Now there are all kinds of fun tricks and techniques for polarizing light in different ways. You can have it polarized linearly. You can have it polarized dynamically so that the electric field and magnetic field directions contorts around the beam as it moves. You can pass it through materials like calcite that enhance or enable these effects. But the point is, there are always *two* orthogonal options.

Now light from the sun or whatever comes at us in all kinds of directions. All of them. We say that light’s unpolarized. To to get light polarized with the electric field pointing upwards, we need to pass it through a filter. Something you can put on your sunglasses or camera lens.

Suppose we do.

Now let’s say I pass some light polarized so that the electric field points up through another filter that also points up. What happens? 100% of the light goes through. Ditto if it’s down, you know, flipped by 180 degrees.

But what happens if I rotate that second polarization filter by 90 degrees? The electric field points up, but the filter points sideways. 0% of the light gets through.

Pretty straightforward right. So what happens when I turn that filter by 45 degrees instead? Fans of classical optics now the answer. 50% of the light gets through.

Generically we take the inner product of the two polarization vectors, and get a result that the amount of light coming through depends on the cosine of the angle between them.

Enter the Photon

So far so good, right? So far it’s all been pretty much classical, right? Well here’s a question for you:

We learned that lightwaves are quantized in units of $\frac{hc}{\lambda}$, where $\lambda$ is the wavelength of light. And that’s fine. Individual photons can be polarized. And they are if the light beam is. But what does it mean that 50% of the photons move through the polarization filter?

“Okay...” You might say. “Well then half of them make it through and half are deflected. No big deal.”

Well. Wait a minute. What if we have an odd number of photons? What happens to that last one?

Perhaps now you see the point of why photons make quantum mechanics so weird. You can’t cut that photon in half. Half of that photon doesn’t make it through the filter. Does it?

We do not measure half photons. That’s the whole point of quantum mechanics.

So what happens?

What happens is that individual photons have a 50/50 chance of making it through that polarization filter.

And so now we really understand where that rule that 50% of the light comes through when the angle of the second Polaroid filter is 45 degrees. It’s not that it’s cutting the electric field in half. Each photon has a probability of getting through that’s like 50%.

What’s more. It’s not like exactly half the photons make it through, right? Flip a million coins, you’ll get heads close to half a million times, but precisely a million times? That’s nowhere near as common. There will always be some error.

Indeed, that error is quantified by the binomial distribution. The probability of $p$ photons making it through the polarization filter out of a total of $n$ impinging photons is

$$\mathcal{P}(n;p) = \frac{1}{2^{n}}\frac{n!}{p!(n-p)!}.$$

Sure it looks like a clean 50/50 split when you have a gazillion photons. But that’s an enormous amount of information. What happens when you have 10 photons?

We have less information. We have more uncertainty. We have noise. This is how we can begin to think about Quantum Mechanics.

Oh, and By the way, how do we know that we have exactly 10 photons anyway? More soon.

Exercises

Exercise 1 : Compute the standard deviation of the binomial distribution as a function of $n$.

Exercise 2 : Let's consider the binomial distribution when precisely half the photons make it through. We can then parameterize the total number of photons as $n = 2p$.

$$\mathcal{P}(2p;p) = \frac{1}{4^{p}}\frac{2p!}{p!p!}.$$

Evaluate this probability for $p=5$ and $p=10$.

For large values of $p$ - like the case when we have a gazillion photons - we can approximate the factorial symbol $p!$ as

$$p! \rightarrow \sqrt{2\pi p}\left(\frac{p}{e}\right)^{p},$$

where $e$ is merely the exponential function of $1$. This is the Stirling Approximation, and it is mean to hold asympototically for large values of $p$. Evaluate the binomial distribution using the Stirling Approximation for both $n = 2p$ and for generic $n$.

Exercise 3 : For more practice with the Stirling Approximation, evaluate the binomial distribution for the case where only a handful of photons make it through the filter, that is when $n$ is enormous and $p/n \rightarrow 0$.

Exercise 4 : The binomial distribution is modified when the probability of a photon making it through the filter is not precisely 50%. Suppose that the probability is actually given by $q$. Then,

$$\mathcal{P}_{q}(n;p) = \frac{n!}{p!(n-p)!}q^{p} (1-q)^{n-p}.$$

Determine the probability of a photon making it through a polarization filter set at a generic angle $\theta$ (hint: Intensity is proportional to the square of the magnitude of the electromagnetic field). What is the most probable number of photons $p$ that make it through as a function of $\theta$? What is the standard deviation? Apply the Stirling Approximation to see what happens in the limit of large $n$.