Light in a Box

Jun 7

We review the macroscopic properties of light and demonstrate how Quantum Mechanics puts a finite resolution to their energies. We then illustrate how this manifests quantitatively in a cubic radiation cavity.

The two physical parameters we've been discussing are Planck's constant $h$ and the speed of light $c$. In the context of information, $h$ gives a finite resolution to universe's ability to carry information. $c$ represents a maximum possible speed at which that information can flow. We'll explore both of these ideas today explicitly in terms of light.

The Colors of Light

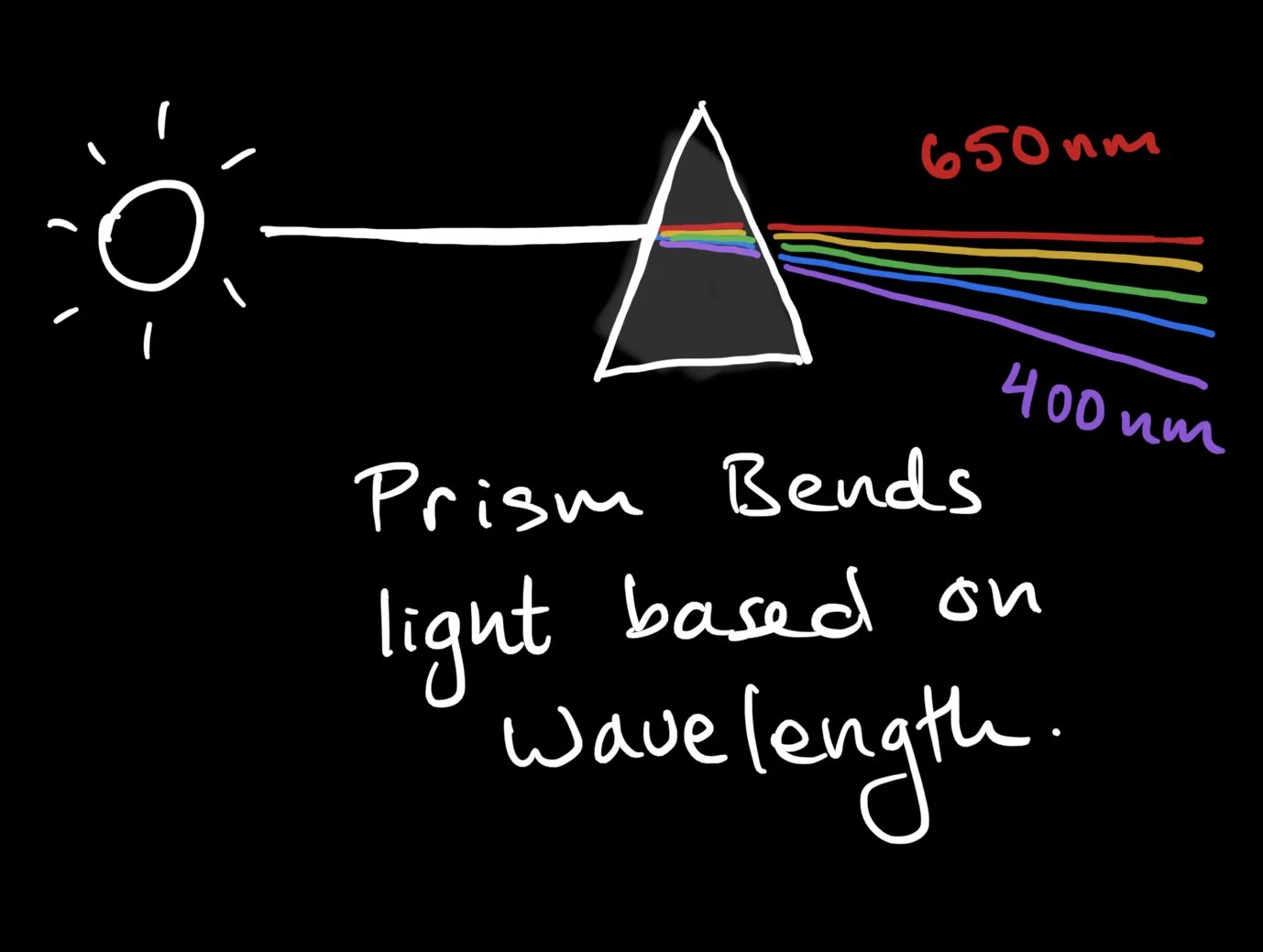
Light is rarely monochromatic. The colors we see outdoors all originate from sunlight. Walk by a tree and observe the green leaves. The chrolophyll in the leaves absorb much of the red and blue light from the sun, reflecting back only the rest. From our perspective, what remains yields different shades of green depending upon the chemical details of the individual trees.

Nevertheless, we can split the colors of sunlight using a dispersive media such as glass or water - that is, a prism. A prism causes light to refract or bend differentially depending upon wavelength. Typically bluer light bends more than red, separating the sun's rays into a rainbow. Water droplets in the atmosphere sometimes serve as us the eponymous example of a rainbow.

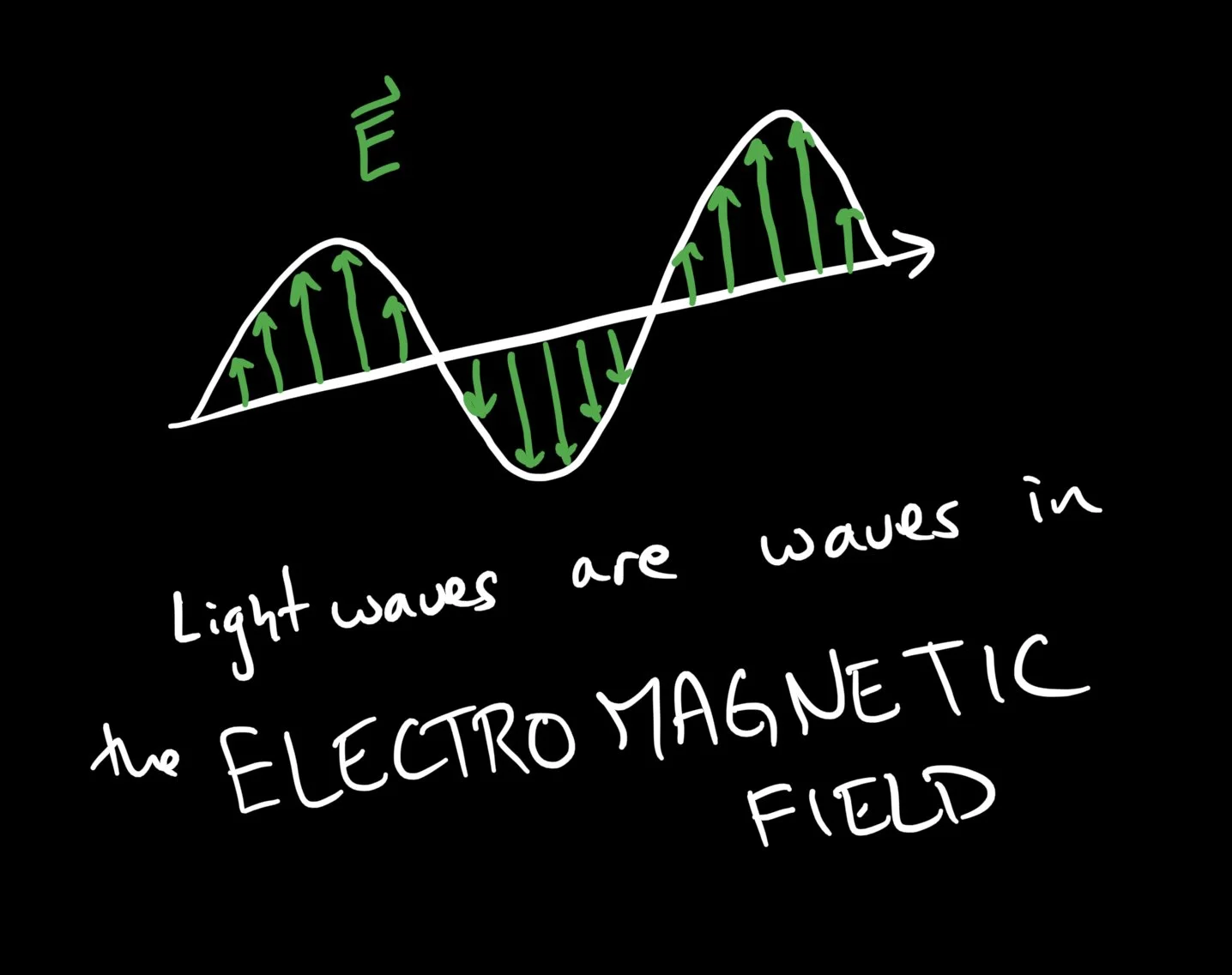
Light itself is a wave comprised of electric and magnetic fields. The individual colors of light correspond to specific wavelengths of those field oscillations. Alternatively, we can assign colors to specific frequencies of light. As with any wave, we have the simple relationship between speed ($c$), wavelength ($\lambda$) and frequency ($f$):

\begin{equation}\label{c}c = \lambda f.\end{equation}

Classically, the amplitude of the electromagnetic wave [$\mathcal{A}$] - the intensity of the light - scales with its energy:

\begin{equation}\label{classicale}E \propto \frac{1}{\epsilon_{0}}|\mathcal{A}|^{2}.\end{equation}

Technically speaking the intensity is proportional to $|\mathcal{A}^{2}|$. But hopefully the point is clear: for an electric lamp with a dimmer switch, you can lower the energy of the light emitted by reducing the electricity going flowing into the bulb.

Particles of Light

Quantum Mechanics tells us that there is a fundamental resolution to light. Light is quantized into packets of discrete energy, and this resolution depends on $h$ and $c$. For light in a given wavelength $\lambda$, the smallest possible energy packet has the energy

\begin{equation}\label{e}E = \frac{hc}{\lambda}.\end{equation}

As might be familiar from last time,

\begin{equation}\label{hc}hc \approx 1240 \,\mathrm{eV}\cdot \mathrm{nm}.\end{equation}

So that the energy of a given photon is inversely proportional to its wavelength, and the constant of proportionality is precisely the factor that signals the breakdown of classical physics.

Alternatively, we may use \eqref{c} to write

$$E = hf.$$

The quantization of light into photons - given by equation \eqref{e} - was a foundational idea in Quantum Mechanics. Importantly, each color of light - given by the wavelength $\lambda$ - has a minimum physical energy, given by \eqref{e}. Light with smaller wavelengths has a larger minimum energy requirement to even exist. Blue light is more costly - energetically - than red light.

This experimentally confirmed fact was not always obvious. To understand how the existence of photons gave rise to Quantum Mechanics, it helps to see how photons resolved an issue in older models of electromagnetic radiation.

Light Waves in a Box

Light is known to be waves in the electromagnetic field. Electric fields vanish on a conducting surface - so a closed, metal box can hold a lot of electromagnetic energy in a relatively predictable way.

Consider the inside of a hollow metal cube whose sides have length $\ell$. Since all electric fields must vanish on the edges of the cube, the longest wavelength allowed inside the box is

$$\lambda = 2\ell.$$

Why twice $\ell$? Because half a sine wave corresponds to the lowest possible mode.

$$\sin(n\pi) = 0,\quad n = 0,1,2,\cdots.$$

For such an electromagnetic wave, the electric field will look something like

$$\mathcal{E}_{1} \sim \mathcal{A}_{1}\sin\left(\frac{\pi x}{\ell} \right)$$

In general such an electromagnetic wave will have components in all three spatial directions as well as time. We can save those details for a course on electromagnetism. For now the symmetry of the box allows us to focus on what's most important: $\mathcal{E}_{1}$ represents the lowest frequency electric field allowed. We can include many more. In principle infinitely many more, as

\begin{equation}\label{electricN}\mathcal{E}_{n} \sim \mathcal{A}_{n}\sin\left(\frac{\pi n x}{\ell} \right),\end{equation}

where $n$ is a strictly positive, whole number. This correspond to higher frequency modes of the electromagnetic field, which are also allowed by the shape of the box because they also vanish at the edges. In other words, the allowed wavelengths of electromagnetic energy in this box are:

\begin{equation}\label{boxlambda}\lambda = \frac{2\ell}{n},\quad n = 1,2,3,\cdots\end{equation}

This leads us to an important - if familiar - observation:

The allowed frequencies/wavelengths of a wave is constrained by the properties of the container they belong to.

In a metal box - such as an oven - the colors of light are quantized. But this has nothing to do with Quantum Mechanics, a priori. It's just part of the geometry of the problem. Before the discovery of Quantum Mechanics - before we knew about \eqref{e} - this model had a deep, conceptual problem. Consider the following natural question:

Suppose we heat up such a metal box, so as to give the electromagnetic field inside the box some energy. If we open the box, what do we see?

We know the light will come with discrete wavelengths \eqref{boxlambda}, but how much of each color will we see? Put differently:

If we give an energy $E$ to the electromagnetic field inside the box, how will that energy distribute over the different wavelengths of the electromagnetic field?

Before Quantum Mechanics, it was known that the energy of light waves was proportional to their intensity, \eqref{classicale}. More precisely, the energy inside the box was given by

$$E = \frac{1}{\epsilon_{0}} |\mathcal{A}|^{2} \times \mathrm{Volume}.$$

Since the electric field is a vector, they add together linearly. We also know that light comes with discrete wavelengths parameterized by $n$, we can sum over all the different amplitudes of all the different modes of the electromagnetic field:

\begin{equation}\label{qe}E = \frac{\ell^{3}}{\epsilon_{0}}\sum_{n=1}^{\infty} |\mathcal{A}_{n}|^{2}.\end{equation}

In other words, the energy of the light waves should be distributed amongst the amplitude of the different modes of the electromagnetic field, $\mathcal{A}_{n}$, for each wavelength $\lambda_{n}$.

Of course, this redefines our question but does not solve it:

How does $E$ get distributed amongst the different intensities $\mathcal{A}_{n}$?

The problem facing physicists at the turn of the 20th century was the fact that the energy of these individual modes of the electromagnetic field - was classically the same for each $n$:

$$E = \frac{1}{\epsilon_{0}}\int_{0}^{\ell}dx \left(\mathcal{A}_{n}\sin(\frac{\pi n x}{\ell})\right)^{2} = |\mathcal{A}_{n}|^{2}$$

With no way to distinguish between the modes energetically, there was no way to predict what the inside of the box would look like.

The Ultraviolet Catastrophe

Actually, there was a way to predict what the inside of a box would look like. If the energy of all colors of light were the same, the energy of the light should be distributed evenly amongst them. But given that $n$ ran from 0 to $\infty$, with

$$\lambda_{n} = 2\ell n,$$

there were far more possible modes with large numbers of $n$ than small. Thus, the prediction was that upon opening the oven, the light would all be at the smallest possible wavelengths of the spectrum. Not blue. Not violet. But ultraviolet! In other words, most of the energy in a given metal box should be distributed amongst colors of light that are too small to be seen by the human eye! And this would be true for any value of $E$!

This was not was observed in experiments at all. Rather, the color of light inside such a box changed with the temperature of the box. In simple terms, the average color of light - highest value of $|\mathcal{A}_{n}|^{2}$ - changed with the temperature of the box. In these simple terms, a lower temperature metal box had mostly red light, and a higher temperature metal box would have mostly blue light. Precisely the opposite of what was predicted.

Of course, nobody believed that ``prediction'' - that virtually 100% of the light would be in the ultraviolet range - was true. There was some kind of error in the theoretical model. Some kind of error in the way they understood electromagnetism. At the time, this discrepancy was referred to as the ultraviolet catastrophe.

Photons to the Rescue

The paradox of the ultraviolet catastrophe was resolved with the realization that light was quantized, and that individual colors of light came in packets with a minimum energy that depended on their wavelength: \eqref{e}.

Let

$$\mathfrak{e}_{n} = \frac{hc}{\lambda_{n}} = \frac{nhc}{\ell},$$

be the quantum of energy associated to a photon of wavelength $\lambda_{n}$. Then the fraction of energy $E$ devoted to this color of light must be an integer multiple of $\mathfrak{e}_{n}$. In other words,

$$E = \sum_{n=1}^{\infty} N_{n}\mathfrak{e}_{n},$$

where $N_{n}$ counts the number of photons with wavelength $\lambda_{n}$.

Immediately we notice two things. First, there is a maximum value of $n$, $n_{\rm max}$, such that

$$E \leq \mathfrak{e}_{n_{\rm max}}.$$

This greatly helps to solve the ultraviolet catastrophe paradox by giving a lower bound on the wavelengths that can be inside the box: $\lambda_{n_{\rm max}}$. Thus,

$$E = \sum_{n=1}^{n_{\rm max}} N_{n}\mathfrak{e}_{n}.$$

Second, as the energy grows, the minimum possible wavelength $\lambda_{n_{\rm max}}$ grows smaller.

Careful attention to the mathematical and physical details associated with \eqref{e} results in a prediction that accurately reflects experimental observations.

If you're curious, the average number of photons$^{1}$ of a given wavelength [$\lambda_{n}$] is given by

$$\langle N_{n} \rangle = \frac{1}{e^{\frac{hc}{\lambda_{n}kT}} - 1}.$$

Here $T$ is the temperature and $k$ is a physical constant,

$$k = 8.617333262145 \times 10^{-5} eV / K,$$

where $K$ stands for Kelvin, a unit of temperature.

$k$ is a useful constant that allows us to think of a temperature as an energy, that is $kT$ has units of eV.

Exercises

Exercise 1 (The Photoelectric Effect):

When light shines on the surface of some metals, electrons are released. Often those electrons are collected into a wire and measured as an electrical current. Classical electromagnetism argues that light transfer energy to electrons by oscillations in the electric fields, suggesting that the observed current should depend primarily on the intensity (amplitude) of the incident light wave. Moreover, the classical theory predicts that the speed / kinetic energy of the electrons released should also depend on the intensity of the light.

Curiously, none of this is observed. For a fixed kind of metal, electrons only are released when the wavelength is sufficiently small, no matter how intense the beam of light is. Varying the intensity instead primarily changes the number of electrons released, not their kinetic energy.

Explain why these observations provide physical evidence for the quantization of light into photons.

Exercise 2:

Suppose you collect light from the cubic box described above into a beam and pass it through a prism. Explain qualitatively what you'd expect to see in terms of the colors or frequencies of light. How is this changed as we change the size of the box? In terms of larger values of $\ell$, what would physically constrain our ability to see the discrete pattern in the dispersed light?

Exercise 3:

The ground state of the hydrogen atom has an energy of 13.6 eV. What size box of photons would have this value as its lowest energy state? What would its next three energy levels be?