The Charged Sigma Baryons

The Σ baryons - that’s a capital Sigma - are a trio of slightly heavy cousins to everyday particles like the proton and the neutron.

With masses of almost 1200 MeV each, it may surprise you that the physics of Σ baryons feels much closer to a comparatively puny trio of familiar particles: the pions.

The pions form a triplet of mesons: π⁺, π⁰ and π^-. So too, do the Σs: Σ⁺, Σ⁰ and Σ^-. The similarities are helpful for building an intuition, but the differences are stark. While the charged pions are antiparticle partners, the charged Sigmas are anything but.

Today we’ll focus on that fact as we explore the pair of particles Σ⁺ and Σ^-.

The Charged Sigma Baryons

The charged Σ baryons are your typical strange particle. They live much longer than they should, given their mass. Their lifetime is a sizable fraction of a nanosecond. Like the Λ⁰, the charged Σ baryons live so long because they have to wait for their constituent strange quark to decay.

The strange quark can only decay to an up quark, and while possible, it takes a while. It’s a quantum bottleneck that in particle decays that has come to be known as the technical term “Strangeness”.

While the down quark and the strange quark have separate identities as far as the strong nuclear force is concerned, they mix slightly under the weak nuclear force. That slight mixing is what gives the strange quark a chance to decay.<

And it always decays to an up quark.

Keep an eye on this fact. It’s what makes the Σ baryon decays so tricky.

What’s fun about the charged Σ Baryons - that is markedly different than the charged pions - is that they are not antiparticles for one another. The antiparticle, Σ(bar)+ is not the Σ^-. Not even close.

The Σ⁺ has two up quarks and a strange quark. That gives it’s electric charge of 2/3+2/3−1/3 or one. The Σ^- has two down quarks and a strange quark, which contribute a charge −1/3 each.

So, despite having opposite electric charges, they have very different quarks inside: up-up-strange versus down-down-strange. And with that constitutional difference comes more mundane ones: the Σ⁺ and Σ^- have slightly different masses and slightly different lifetimes. They are, in other words, very different particles.

Figure: Charged Σ Baryon Decays.

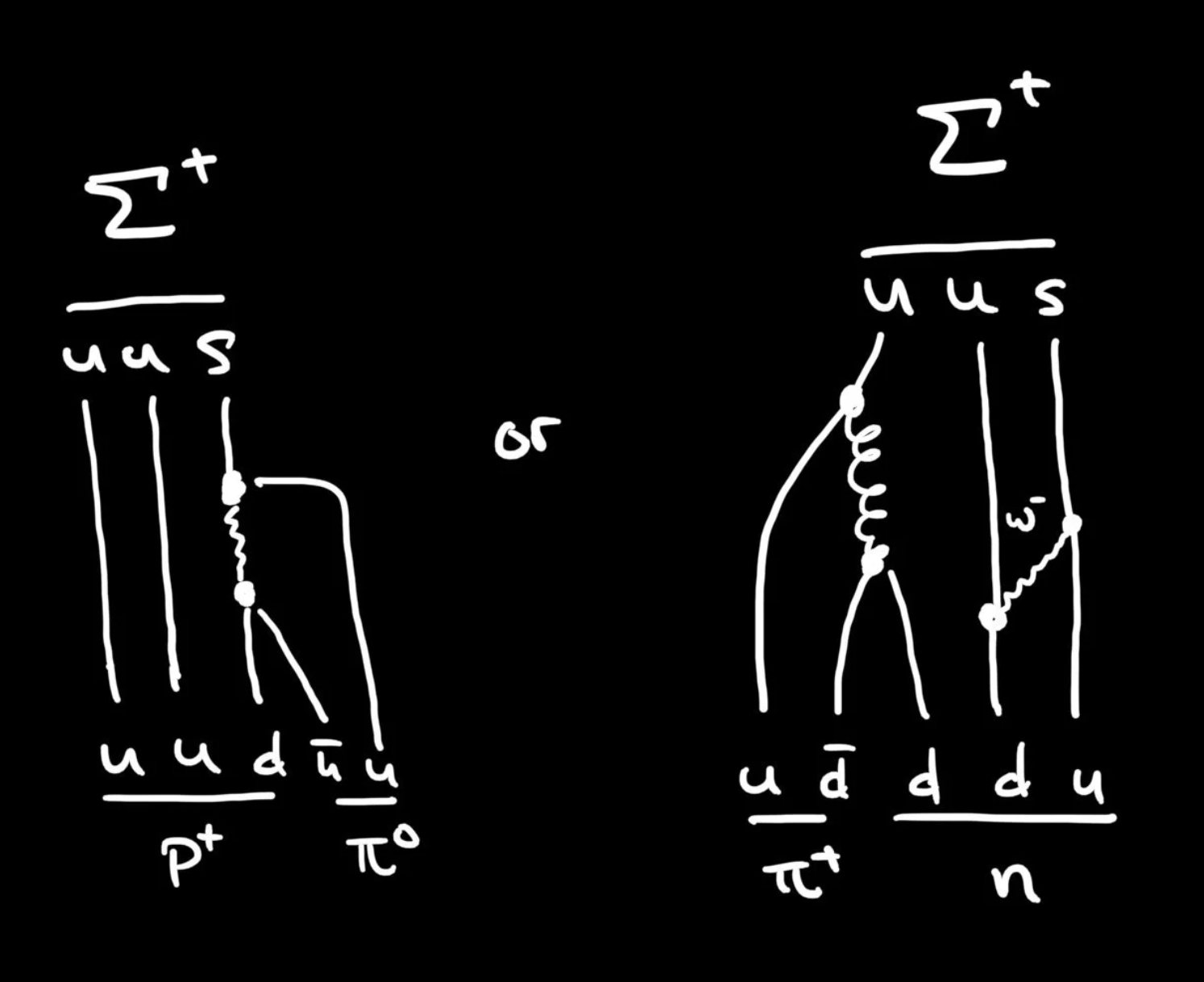
The charged Σ baryon has a number of options for decays in relatively similar ways.

Still. The Σs try their best to behave like pions. Isn’t it nice how neatly organized Nature at least tries to be?

At 1197 MeV, the Σ^- is just a little bigger than the Σ⁺, whose mass is about 1189 MeV. Bigger masses usually imply short lifetimes, but the Σ Baryons are strange in this sense too. The heavier, Σ^- baryon has a lifetime around 15% of a nanosecond. The lighter Σ⁺ baryon decays about twice as fast, living on average for about 8% of a nanosecond.

Decays

Why does this slightly lighter, Σ⁺ baryon decay twice as fast?

Σ⁺ has two major ways to decay whereas Σ^- has only one.

Σ^- only really decays to a neutron and a π^-:

Σ −→ n + π^-

There are other options - including muons, electrons, neutrini and, rarely, a Λ⁰-electron pair - which all together occur less than 1% of the time.

Similarly, 99% of the time Σ⁺ will decay into a familiar nucleon and a pion. But here’s a slight imbalance between these two options. The proton and π⁰ appears just over 51% of the time:

Σ⁺→p⁺+π⁰

The neutron and π⁺ happens a bit of 48% of the time:

Σ⁺→n+π⁺.

Amusingly, the other 1% of stuff looks exactly like the antiparticle versions of the rare Σ^- decays. You know, antimuons, positrons and neutrinos. Notably, there’s also a rare Λ⁰ with positron decay:

Σ⁺→Λ⁰+e⁺

Charge has to be conserved, after all.

Because the Σ⁺ has two ways to decay - two decay channels, in the parlance of particle physics - it’s not surprising that it decays twice as fast as its negatively charged sibling.

Why the Σ^- only has one decay channel relates back to the fact that is not the antiparticle partner of sigma plus. Despite its negative charge, it’s made of quarks and not antiquarks. Because there is no negatively charged analog for the proton, there’s nothing else for the Σ^- to decay into.

The Gory Details

The details of these decays are fun to examine.

The sigma minus - down, down, strange - decays when the strange quark does. The strange quark emits a W-boson and leaves behind an up quark. That essentially converts the Σ^- into a neutron: down-down-up. The W-boson promptly decays into a down-antiup quark pair, that is, a π^-.

The Σ⁺, whose valence quarks are up-up-strange, is a bit more complicated. The strange quark again decays, but the final combination of quarks: up-up-up-down-antiup, can be rearranged to form a proton: up, up, down and a neutral pion: up-antiup. Because the W-boson lives for such a short time, that rearrangement all essentially happens at once.

The other possibility for the Σ⁺ is even more wild. The strange quark decay as usual, laving behind an up quark, but the emitted W-boson is immediately absorbed by one of the other up quarks, which is converted into a down quark. If a gluon just happen to be emitted at around the same time, it can convert to a down quark-anti-down quark pair, giving a final combination of quarks: up-down-down-anti-down-up. This can be rearranged to form a neutron: up-down-down, and a π⁺: up-anti-down.

Was that complicated enough for you? Converting a Σ⁺ to a neutron is a little more complex so it doesn’t happen quite as often. But suffice it to say, gluons aren’t hard to find given all that nuclear goo those quarks live with. It’s not all that surprising things work out this way.

We should say that these descriptions are something of a sketch or skeleton of what is actually going on. Physicists doing the full calculation using Quantum Field Theory would call it a tree^-level approximation. Quantum effects can sometimes be dramatic, as we saw with the π⁰. Mercifully, not in this case.

Particle physics is nothing if not messy.

Why no Lambda Zero

If you’re numerically minded - like you accountants out there - you might wonder why these charged Σ baryons do not decay into a Λ⁰ baryon. After all, the mass of the charged Σ is around 1190 MeV, but the mass of the Λ⁰ is only just shy of 1116 MeV.

Energetically, it’s more than possible! But the details matter.

Both Σ⁺ and Σ^- can and do decay to Λ⁰ with either a positron or an electron, respectively. But it’s a needle in a haystack. For every million charged Σ baryons you produce - say from cosmic rays in the upper atmosphere or at a particle collider - you can probably count the number of Λ⁰’s produced on one hand.

Why is it so rare? Well the strange quark - slow as it is to decay - decays to an up quark much, much faster than the down quark does. Like a few parts per million times faster.

So the statistics all wash out, in the end.

Next Time, while the charge sigmas have trouble decaying into a Λ⁰, the Σ⁰ baryon does not. This leads to another fun story, which we’ll visit next time.