The Delta Baryons

The Delta baryons are combinations of up and down quarks. They’re like the proton and the neutron, only much more heavy and much less stable. They all seem to have about the same mass - around 1232 MeV, but we don’t really have a good handle on it. That is mostly because the Delta baryons lives are so short. They decay extremely quickly - 5.6×10⁻²⁴ seconds.

There are four delta baryons, corresponding to all triplet combinations of up and down quarks:

Δ⁺⁺ = uuu,

made from three up quarks, which has an electric charge of +2e.

Δ⁺ = uud,

made from two up quarks and a down, which has an electric charge of e.

Δ⁰ = udd,

made from one up quark and two downs, which is electrically neutral.

Δ^- = ddd,

made from three down quarks, which has an electric charge of −e.

What makes these combinations different from protons and neutrons is their spin. The uud of the Δ⁺might look like a proton, but it has a higher intrinsic angular momentum. The quarks are zooming around each other - and all that subnuclear goo - with more energy than they do in the proton, which explains the higher mass.

In other words, Δ baryons are excited states of the proton or neutron. And excited states decay. They decay so quickly because the strong nuclear force - the same force that holds them together - is so strong.

Figure: The Delta Baryons

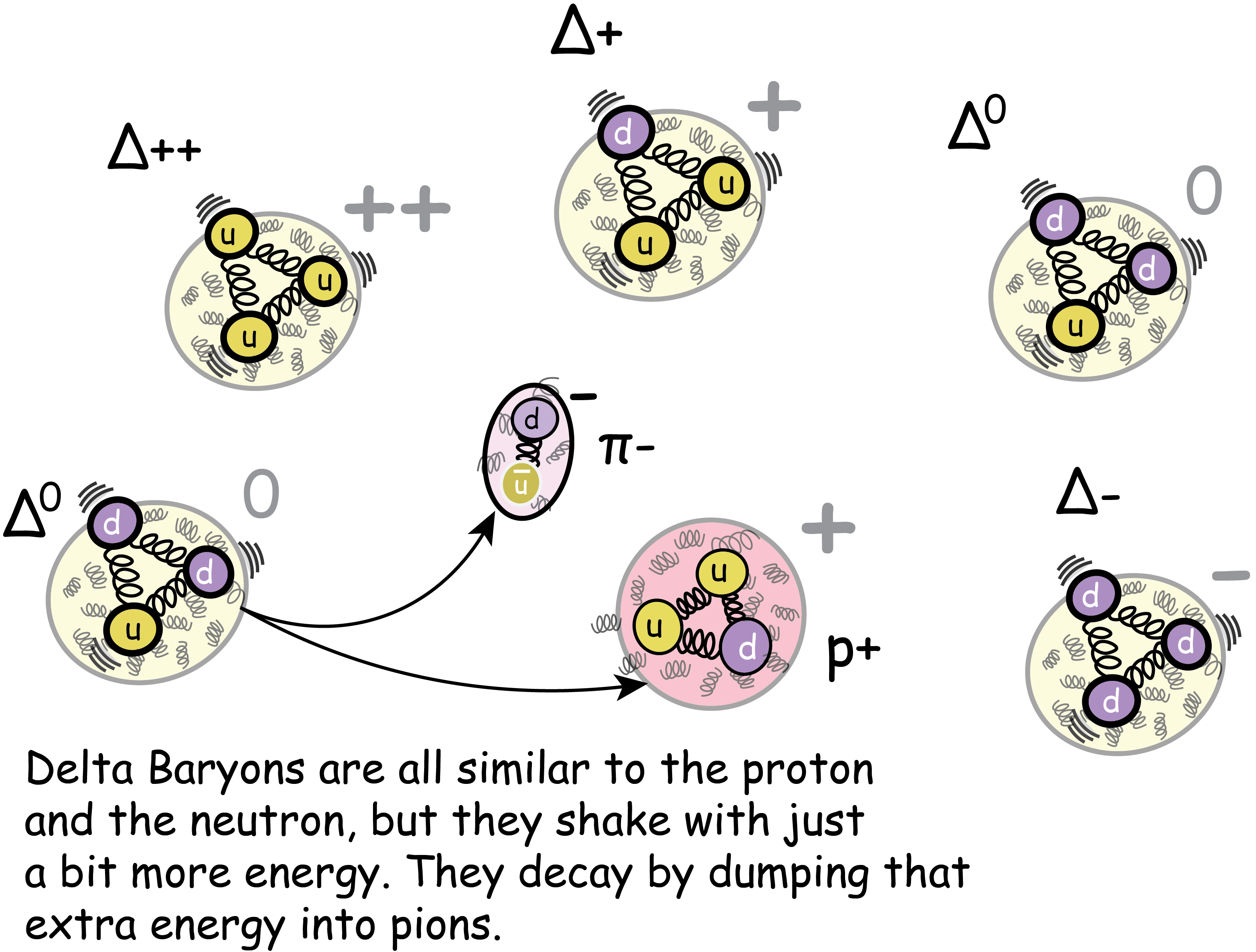
There are four seperate particles, grouped in threes, whose identity depends on their quark constituents.

Figure: Δ⁺⁺ Decays

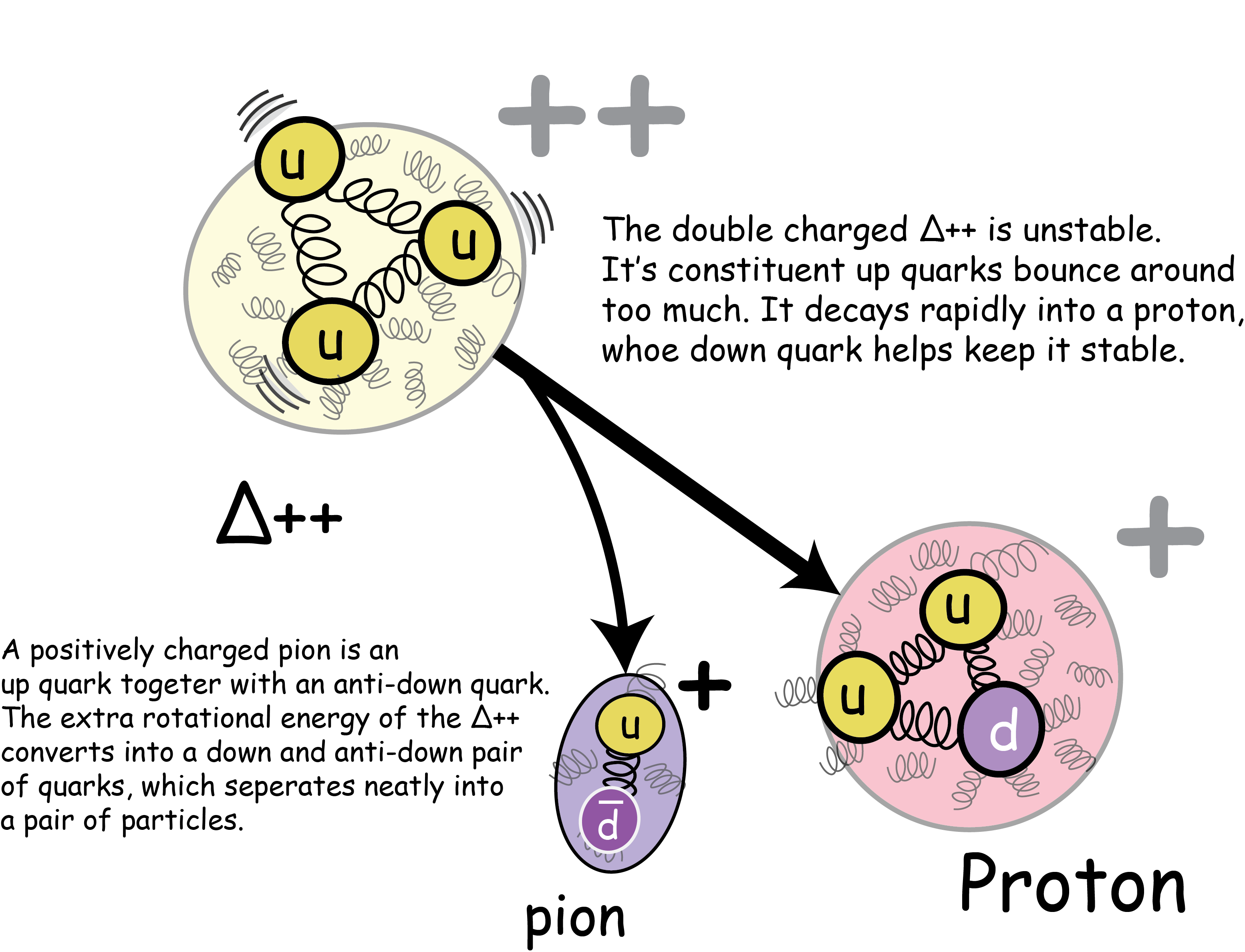
The Δ baryons are heavy and unstable, they decay to particles like the proton.

The electron cloud of an atom can be similarly excited: their electrons can bounce up to a higher energy orbital state, often with more angular momentum. When they decay, they tend to emit photons. If you’ve seen glow in the dark toys - or pictures that glow under UV light - you’ve seen electron cloud decays with your own eyes.

The Δ baryons decay similarly, although being bags of quarks they emit pions. Δ⁺⁺ decays to a proton with a charged pion conserving electric charge:

Δ⁺⁺ → p⁺+π⁺.

Δ⁺ typically decays to a proton and neutral pion:

Δ⁺ → p⁺+π⁰.

Rarely, it will decays to a neutron instead,

Δ⁺ → n⁰+π⁺.

but you get the main idea: electric charged is conserved. Δ⁰ converts to two neutral particles, the neutron and neutral pion:

Δ⁰ → n⁰+π⁰.

The Δ^- decays to a neutron and an oppositely charged pion,

Δ^- → n⁰+π^-.

Delta baryons play a crucial role in limiting the speed of cosmic rays. Cosmic rays are mostly comprised of protons flying through deep space - some at outrageously high velocities. Once those protons are accelerated up to enough energy - 5×10¹⁹ eV - which is about the kinetic energy of a child walking (contained in single particle!) - they tend to collide with the photons left around from the Big Bang. Those collisions, from the perspective of those ridiculously fast protons, are extremely energetic, and Δ baryons are produced. These of course decay almost immediately into proton, neutrons and pions, effectively converting that stupidly high kinetic energy into pion radiation. In other words, intergalactic friction in the universe is provided by Δ baryon production and decay.

Of course, we still see a few cosmic rays with energies far beyond that limit, so it’s not a perfect speed limit, but a pretty effective one.