
The Cascades (Ξ Baryons)
Charge and Mass
Prepare for trouble! And make it double! Today we confront the two Cascade or Ξ ("ksee") baryons which each have a pair of strange quarks.Ξ- checks in with a mass of about 1322 MeV, making it the heaviest baryon we’ve encountered so far. This is just as well, as it comprised of two of those heavier, strange quarks. Together with a third, down quark, it also has a total electric charge of −3/3 or… minus one.
Ξ0 is just a little bit lighter with a mass of 1314 MeV. Its two strange quarks are paired with an up quark, which gives it an electric charge of −1/3−1/3+2/3, or… zero.
Decays of the Ξ-
Like many strange particles, the cascades take quite a while to decay. The Ξ- takes a solid fraction of a nanosecond, the usual time it takes to convince one of those strange quarks to decay into an up quark. The result? The strange-strange-down bag of quarks converts to up-strange-down bag, otherwise known as the Λ0 baryon. As usual, that decay is accompanied by some other junk, and in this case the net result is a π−.As we’ve already seen, the Λ0 and the π- are both unstable themselves. The former converts to either a proton or a neutron and the latter typically decays to a muon and then an electron.
If you tried to sketch that all out, you’d find a long decay chain with a lot of different particles. This gives the cascades their name. Producing just one Ξ-baryon results in a cascading shower of particles all the way down to familiar, stable stuff like protons, neutrons and electrons (and their accompanying neutrini).
Now the Ξ- almost always decays to the Λ0 with a π−. Like 99.8 percent of the time! The rest of the time we find some cuter decays, each incredibly rare, happening less than a thousandth of a percent of the time.
These rarer decays shed some rather alarming light on the very identity of the strange quark. But before we get to that, we should talk about the Ξ0 .
Decays of the Ξ0
The Ξ0 takes about twice as long as the Ξ- to decay, which is still, only a third of a nanosecond. What’s short for humans is a seriously overripe old age for an elementary particle.Like it’s partner, the Ξ0 decays into a Λ0 with a pion. This time a neutral pion. This happens 99.5 percent of the time. These decays are a little twisted.
Its is the same thing we saw with those charged Σ-baryons. We need to convince an a bag of of three quarks: up-strange-and-strange, to decay in something that looks like the up-down-strange bag of the Λ0. This is troublesome precisely because the strange quark only ever decays to an up quark.
As with decays of the Σ-baryons, things just need to rearrange a little bit. The Σ+ you might recall decays into a proton and a π0 thanks to a W-boson. Similarly, one strange quark of the Ξ0 decays to an up quark by emitting a W- boson. The W- decays to a down-anti-upquark pair so fast the rest of the quarks barely notice. The down quark runs away with the other “up and strange” quarks from the original Ξ0 , and the anti-up quark leaves with the freshly minted up quark as a neutral pion.
If that sounds convoluted, it is.
Figure: Cascade Baryon Decays
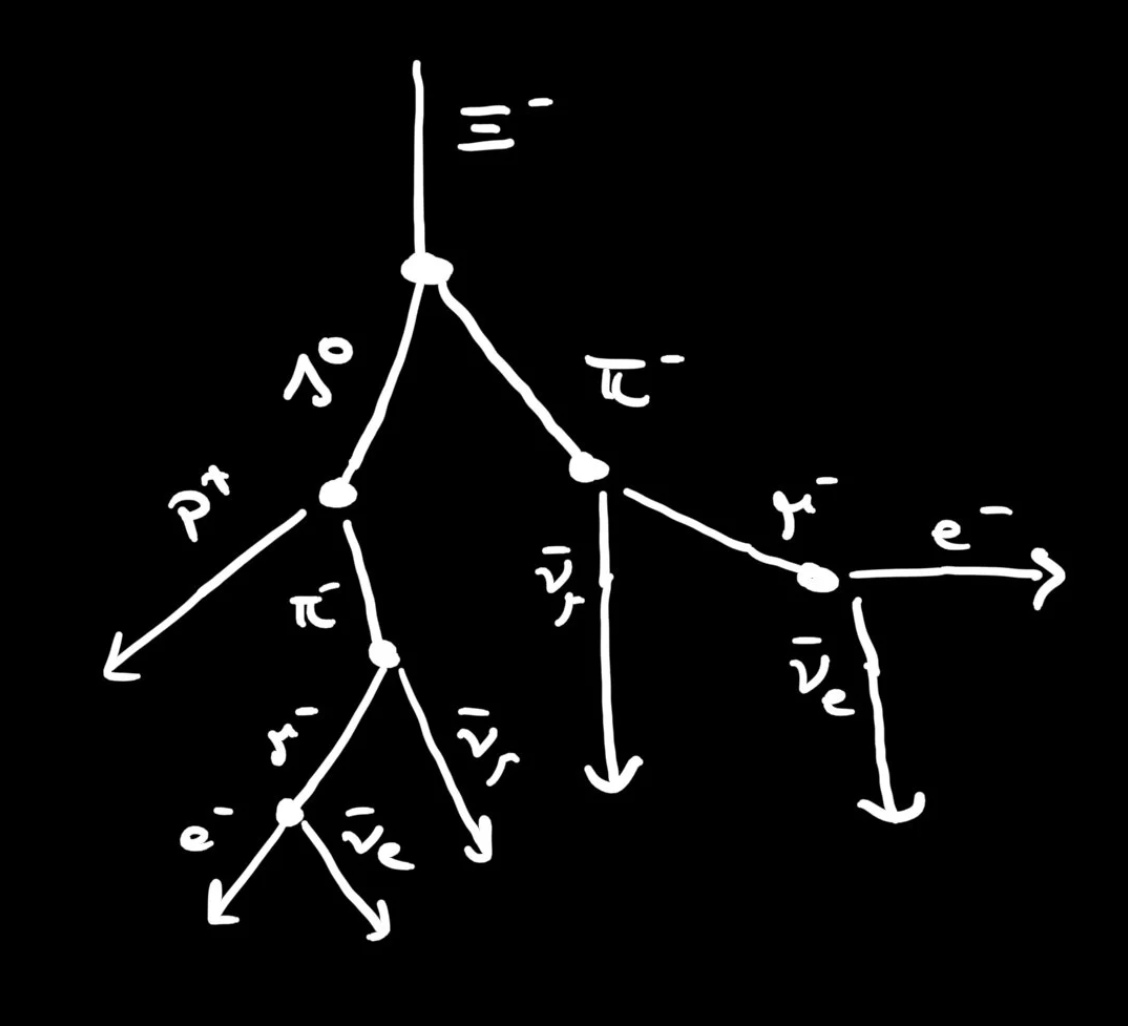
They're called cascades for a reason.
Figure: Initial Phase of the Cascade Baryon Decay
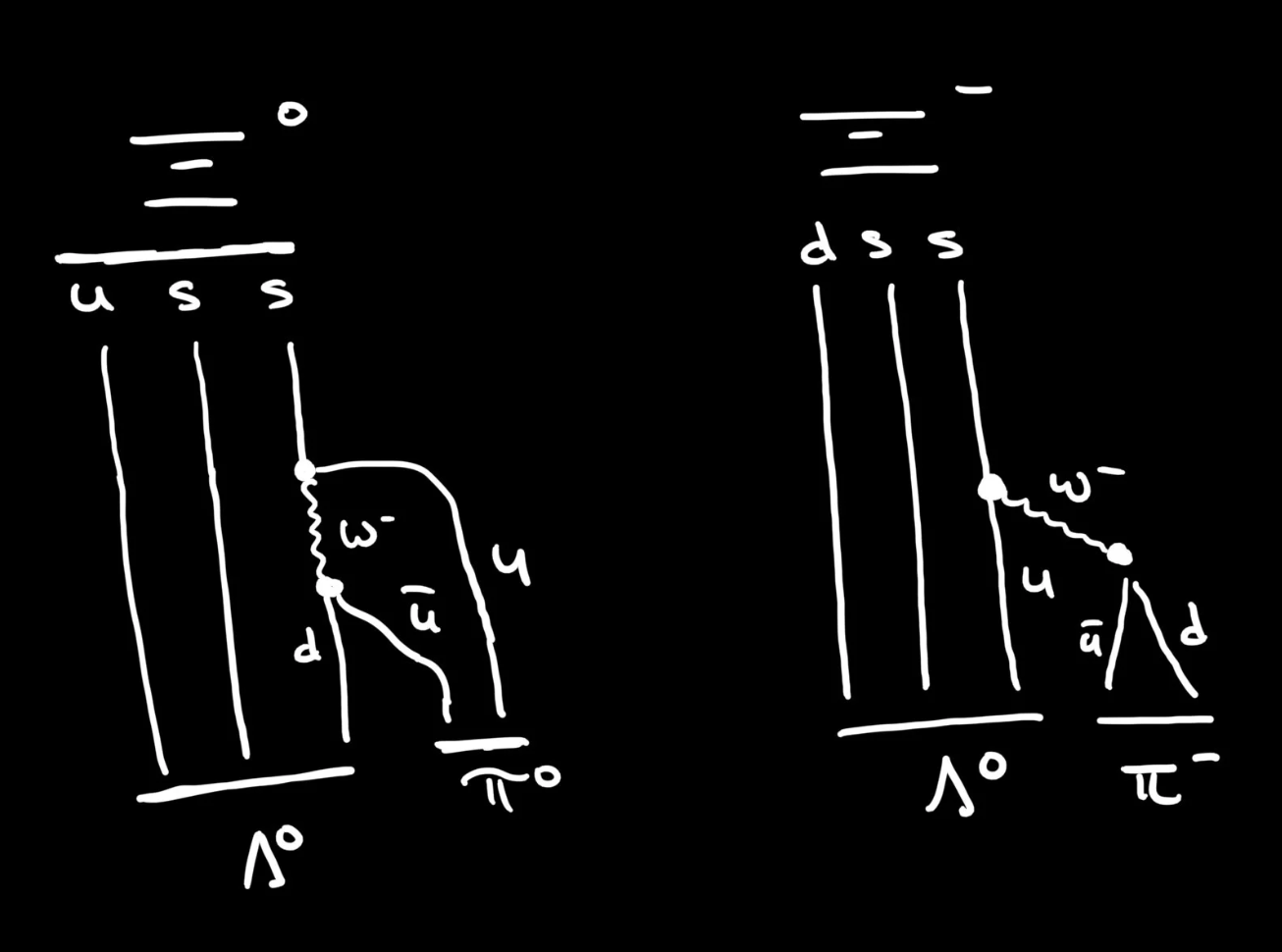
Both the neutral and charged Ξ baryons decay along a similar pattern. It's just they decay into really unstable particles themselves.
Incidentally, the other, rarer decays of the Ξ0 match up quite nicely what you’d expect from those rare decays of the Ξ- . More on those in a later episode.
Spin Angular Momentum
The spin angular momentum of both Ξ0 andΞ- is simply ℏ2, just like the proton and the neutron. Actually, its quite like the proton, the neutron, the three Σ-baryons and the Λ0.That’s a total of eight distinct particles, which is a lot, but you can rest easy knowing there are no other particles with that spin angular momentum made from combinations of those three quarks. And this is no accident.
Any other, three particle combination of up, down and strange quarks - like a baryon with three of the same quarks, like the Δ-Baryons we’ve already seen or a particle with higher mass - will have a higher spin angular momentum.
You could think of that as if the quarks were orbiting each other inside that subnuclear goo at a faster and faster pace. And we’ll meet some examples of these soon enough.
The story behind why this should be is fascinating, nerdy and otherwise adds some useful scaffolding to an ever expanding zoo of wild, subatomic particles.
More on that, next time.